News Story
Path planning for bridge inspection robots
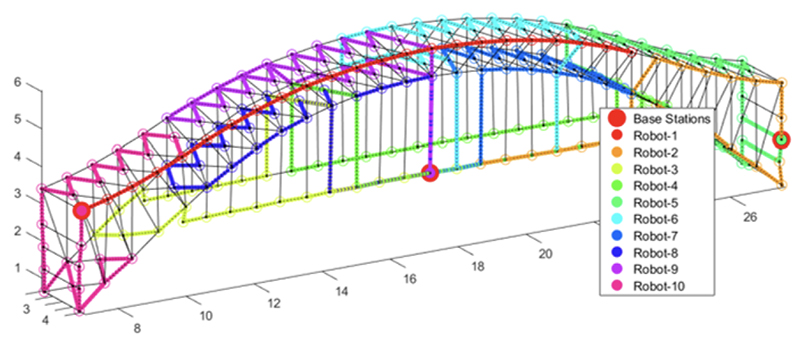
Bridge inspection by mobile robots. (Fig. 1 from the paper)
As civil infrastructure ages, ensuring the safety of structures like bridges, roads and tunnels has become a social imperative. Monitoring existing structures is especially important, as inadequate monitoring can lead to major incidents, such as the collapse of the Ponte Morandi bridge in Italy in an August 14, 2018 rainstorm, which killed 43 people.
The problem is especially acute in the United States, where, according to a 2018 U.S. Federal Highway Administration (FHWA) report, nearly half of all 616,000 bridges are in “fair” condition or worse, and more than 47,000 (7.6 percent of all bridges) are labeled as in “poor” condition. Many Americans well remember the 2007 collapse of the eight-lane Bridge 9340 across the Mississippi River in Minneapolis which killed 13 people and injured 145.
Unfortunately, many segments of bridges are not easily accessible, making it difficult for human inspectors to perform frequent inspections. Budget cuts also limit the number of human inspectors and the frequency of their inspections. As a result, many bridges are not inspected frequently enough to ensure their structural health and safety.
New research by ECE Ph.D. student Michael Lin and his advisor, Professor Richard La (ECE/ISR) contributes to the relatively new idea of using teams of small mobile robots to inspect bridges and other structures. Such robot teams would “live” on the bridge in strategically located depots, from which they would set forth for routine inspections of difficult-to-inspect areas, and to which they would retreat for recharging afterwards. Lin and La’s paper, Miniature Robot Path Planning for Bridge Inspection: Min-Max Cycle Cover-Based Approach, develops a new algorithm to position depots where robots would be stored and recharged, and determines a set of sites for each robot to inspect.
Because such robots would be battery powered and need recharging, their ranges and the tasks they could perform would be limited. The authors considered these energy constraints when considering their planning problem. They formulated their research as a rooted min-max cycle cover problem, in which the vertex set consists of the sites to be inspected and robot depots, and the weight of an edge captures either the amount of time needed to travel from one end vertex to the other vertex or the necessary energy expenditure for the travel. They considered that in the first case, the objective function was the total inspection time, whereas in the second case, the objective was the maximum energy expenditure among all deployed robots. They required that, upon completing the inspection of all assigned sites, the robot must return to the same depot where it is stored. Lin and La then developed a novel algorithm to address these situations.
The problem is formulated as a variant of the uncapacitated rooted min-max cycle cover problem. Each cycle in the cycle cover, which is rooted at a depot, is assigned to a robot and determines a subset of sites that the robot must inspect as well as the depot at which the robot is to be stationed. Lin and La’s formulation of the cover problem assumes that depots are large enough to house as many robots as needed. They suspect that any good solution will distribute the robots evenly across a bridge to minimize the max cycle weight. In some cases, however, the depots may have limited slots for the robots for housing and recharging. Recognizing this constraint, they realize they may wish to reformulate the problem as a capacitated rooted min-max cycle cover, and are currently working on this problem.
Published April 17, 2020